|
Dr. David Berners (left) is the Universal Audio Director of Algorithm Development; Dr. Jonathan Abel is the co-founder and CTO
|
by Dave Berners
Webzine readers want to know, "Why do tubes make even harmonics, and solid-state circuits only make odd harmonics?"
For purposes of this discussion, we will consider the use of tubes and semiconductors as memoryless nonlinearities. By this, we mean nonlinear elements whose outputs at any instant in time depend only upon their input values at the same instant in time. In other words, memoryless nonlinearities do not "remember" anything about the history of the signal being presented to them. In the case where tubes or transistors are used within feedback loops that have filtering (equalization) in the feedback paths, the overall system will not be a memoryless nonlinearity. However, the production of even vs. odd harmonics, in the context of this question, can be most easily elucidated by the study of memoryless nonlinearities.
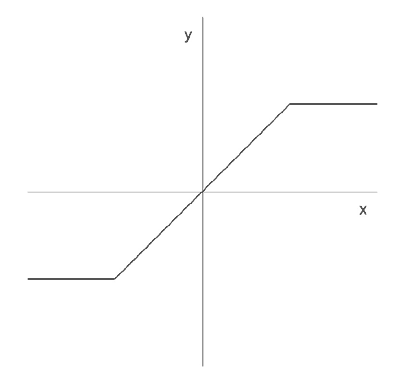
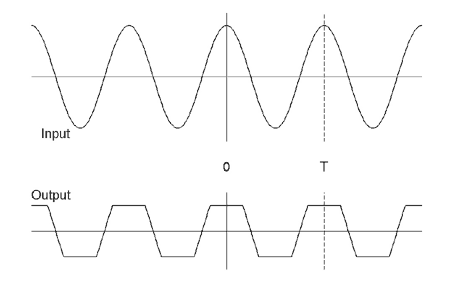
To that end, consider Fig. 1, which shows the input-output relationship for a memoryless, nonlinear system as a function: y = f(x). If an input value x0 is applied to the system, the output of the system will be y = f(x0). The plot in Fig. 1 corresponds to a symmetric clipping element, where the absolute value of the output is bounded by a certain value. Figure 2 shows plots of a sinusoidal input and its corresponding output for the system of Fig. 1.
 |
|
Figure 1: Nonlinear "clipping" function.
|
 |
|
Figure 2: Signal before and after nonlinearity of Figure 1.
|
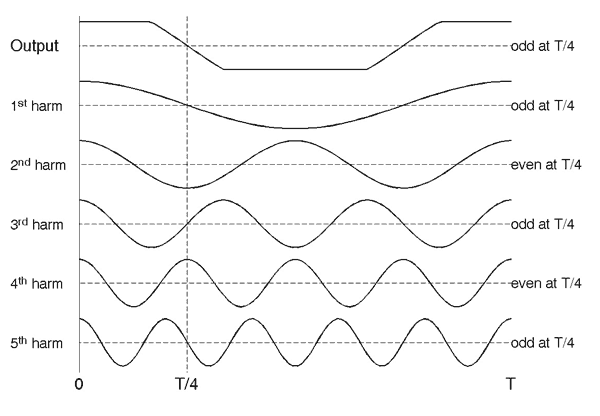
The presence or absence of odd and even harmonics in the system's output can be determined entirely by the shape of that system's nonlinearity (Fig. 1). For a periodic input with period T, the system will produce an output that is also periodic with period T, regardless of the shape of the nonlinearity. In this case, the distortion consists entirely of harmonic distortion. Because the output signal is periodic, it can be represented by a Fourier series, as shown in Fig. 3. In general, the components of a signal's Fourier series are the set of all sine and cosine functions having period T/n (and frequency n/T), where "n" is an integer between one and infinity. The Fourier representation of a signal is formed by adding together scaled copies of the sine and cosine functions in the series. So long as the signal meets certain continuity conditions, the Fourier representation can be made arbitrarily "close" to the signal itself. Figure 3 shows the signal and several of the cosine functions that may be present in the signal's Fourier series.
 |
|
Figure 3: Signal and possible Fourier components.
|
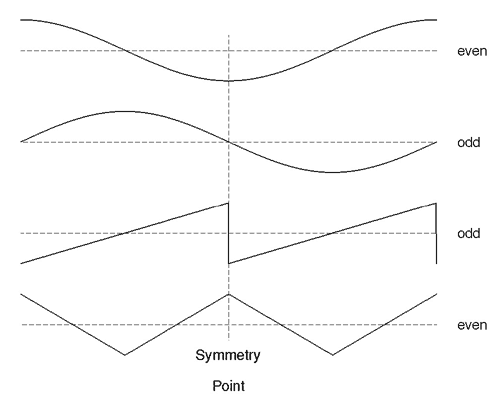
The set of sine and cosine functions (harmonics) that must be included can be determined by looking at the symmetry of the waveform being studied. A waveform is said to be symmetric if there is some "mirror point" within the signal, a point from which the signal looks the same extending in either direction. In other words, the signal to the left of the mirror point is the same as the signal to the right of the point, only flipped backward in time. A signal is antisymmetric if the signal to the left of the mirror point is the same as the negative of the (flipped) signal to the right. Truly symmetric signals are said to have even symmetry, while antisymmetric signals are said to have odd symmetry. Figure 4 shows examples of even and odd symmetric signals and their points of symmetry.
 |
|
Figure 4: Odd and even functions.
|
For signals that have even symmetry about zero (such as the system output shown in Fig. 3), only cosine functions are needed because they are even functions, whereas sine functions are odd about zero. Thus, only the set of cosine functions is shown in Fig. 3. It can be shown that, no matter what the shape of a memoryless nonlinearity, if the input signal is even about time zero, the output signal will also have even symmetry about zero. Thus, for the example of Figs. 1 to 3, both the input and output signals will have even symmetry about zero.
Now, let us examine the symmetry of the output signal around the point T/4. As can be seen, the output signal has odd symmetry about this point. This odd symmetry further reduces the components necessary to construct the Fourier series for this signal. As can be seen from the figure, all odd harmonics have odd symmetry about the point T/4, while all even harmonics have even symmetry. Thus, for signals that have even symmetry about t = 0 and odd symmetry about t = T/4, only odd harmonics of the cosine function are necessary to construct the Fourier series for this waveform. Figure 5 shows an approximation of the output using the first five odd harmonics.
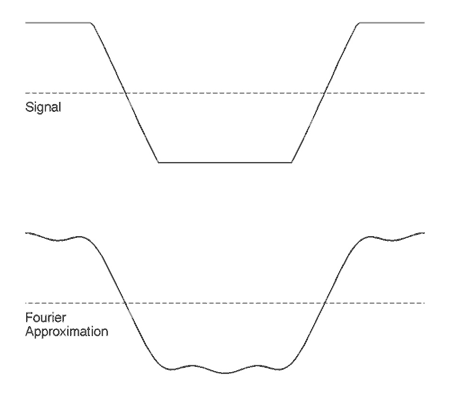 |
|
Figure 5: Signal and Fourier approximation.
|
Having seen how the symmetry of the output signal is related to the presence or absence of harmonics, we now would like to relate the symmetry of the signal to the symmetry of the function describing the nonlinearity. As mentioned above, points of even symmetry in the input waveform will always correspond to points of even symmetry in the output waveform, no matter what the shape of the nonlinearity. For points of odd symmetry in the input waveform, the shape of the nonlinearity determines the symmetry of the output. If the function f(x) describing the nonlinearity is even about zero, a point of odd symmetry in the input will result in a point of even symmetry in the output waveform. If, on the other hand, f(x) is odd about zero, a point of odd symmetry in the input will result in a point of odd symmetry in the output. If the function f(x) has neither odd nor even symmetry about zero, a point of odd symmetry in the input will not produce a point of symmetry in the output.
To summarize, if the function f(x) is odd, a cosine input will produce no even harmonics. If the function f(x) is even, a cosine input will produce no odd harmonics (but may contain a DC component). If the function is neither odd nor even, all harmonics may be present in the output.
The function f(x) in Fig. 1 is a typical nonlinearity for an op-amp. Op-amp circuits typically have strong negative feedback to linearize the circuit up to the supply voltage, but then "clip" the signal beyond that point. Obviously, the function in Fig. 1 is odd, so that this nonlinearity will result in output signals that have no even harmonics. Figure 6 shows a nonlinearity typical of a Class A tube amplifier stage. This function is neither odd nor even, so that both even and odd harmonics will be present in the outputs of this system. But this type of nonlinearity is not displayed only by tubes. Discrete Class A solid-state circuits will often produce similar nonlinearities. The absence of even harmonics is more attributable to circuit topology (e.g., amount of feedback, amplifier gain, number of stages) than it is to circuit technology (e.g., tube or solid-state). However, because of the small size and low cost of solid-state components, it is common for them to be packaged into op-amps, where they are used with high levels of negative feedback. These systems tend to have odd-symmetric relationships between input and output signals. Because of this, absence of even harmonics has often been (wrongly) attributed to solid-state technology.
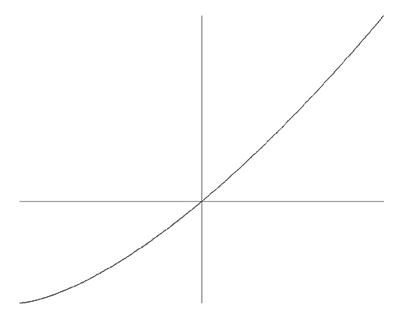 |
|
Figure 6: Typical tube-like nonlinearity.
|