This seemingly innocent question requires a bit of filter theory to answer, and this month's column is the second part of a two-part answer. In the first part, we looked at what "phase" means in the context of equalization and discussed some of the psychoacoustics of EQ phase perception. Here we talk about linear phase and minimum phase filters and their applications to mastering.

Part II: Linear Phase and Phase Conscious Filter Design

As we discussed last time, clean EQs, reverbs, and the like are examples of linear time invariant or LTI systems. Such systems may be characterized by how they respond to a sine wave, and in particular, how they change its amplitude and phase.

 

Let's take a look at the system G{·}, which amplifies an input sinusoid at frequency f by a(f ) and shifts its phase by f (f ),

 

(1)                                    a(f ) sin(2pf ·t – f (f )) = G{sin(2p f t)}.

 

The delay through the system t (f ) experienced by any frequency f is the phase divided by the frequency in radians per second,

 

(2)                                                    t (f ) = f (f ) / 2pf .

 

Now, what happens if the phase f (f ) is proportional to frequency – i.e., if the filter is linear phase? If the constant of proportionality is 2pd, we have

 

(3)                                                       f (f ) = 2pf · d,

 

and we see that a linear phase system delays each frequency the same amount d,

 

(4)                                  t (f ) = f (f ) / 2pf = 2pf · d / 2pf = d.

 

If there is any other relationship between frequency and phase, different frequencies will be delayed different amounts, and we say that there is "phase distortion."

Since phase distortion produces artifacts that people can be sensitive to, attention must be paid to the phase response f (f ) when creating filters. Using analog design, it is impossible to do any filtering without producing phase distortion (many analog designs produce so-called minimum phase systems), but in the discrete-time domain, it is possible to make a filter which has linear phase.

Constant phase delay leads to advantages and disadvantages, depending on the situation. The biggest advantage is gained in filterbank applications, where a signal is split into frequency bands for separate processing, and recombined later. If a filterbank is made to be linear phase, it can be completely transparent as long as no modifications are made to the signal while it is split into separate bands. An application for this may be a de-esser which is being used to limit occasional sibilance. If the de-esser is made with a linear-phase filterbank, it can be made to be absolutely transparent except during those instants when the de-esser is active, reducing sibilance. On the other hand, if the filterbank is not linear-phase, then anything sent through the processor will incur phase distortion all the time, even when no de-essing is taking place. So for transparency in a filterbank, the linear phase property is valuable.

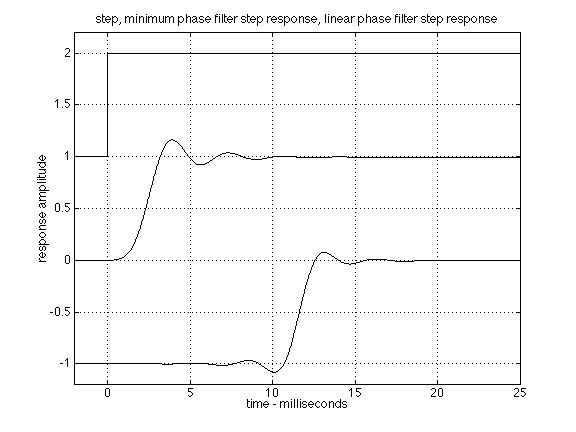
Figure 1

For EQ applications, linear-phase filters will have different properties than their most commonplace counterparts, minimum-phase equalizers, but the advantage is not as clear-cut. Because linear-phase filters delay all frequencies by the same amount, the overall latency for a linear-phase filter will be higher than for its minimum-phase counterpart. Minimum-phase filters, on the other hand, have the least latency for a given magnitude response. This means that linear-phase equalizers can be unsuitable for real-time operation, or for operation within a feedback loop.

Even for offline application of EQ, there can be debate over what phase response is the most desirable. Figure 1 shows the step-response for two lowpass filters with identical magnitude transfer functions but different phase responses (minimum-phase and linear-phase). The latency of the linear-phase filter is clear; its lack of phase distortion is evident in its step response symmetry. See how the artifacts from the transition all follow the transition for the minimum-phase filter, but are spread evenly before and after the transition for the linear-phase filter. Humans are more sensitive to artifacts occurring before the transition, so if a linear-phase filter has noticeable preringing (for instance, if it's a high-Q filter), it might not sound as good as its minimum phase equivalent. For mastering, however, most of the equalization applied is gentle – otherwise it would be fixed in mixing – and the preringing artifacts are minimized. Linear phase filters are then a natural choice because of their lack of phase distortion.

To summarize, in Part One we defined what the phase response is, and gave examples of phase distortion that people can hear. We showed that people can be especially sensitive to phase distortion on transients, and also showed that a given amount of phase offset will produce more time smearing at lower frequencies. In Part Two, we gave examples of where linear-phase filters or minimum-phase filters may be preferred. Linear-phase filters can be ideal for filterbank applications, while minimum-phase filters have an advantage in real-time applications or other situations where low latency is important. For generic EQ applications, minimum-phase and linear-phase filters can sound different, but optimality becomes difficult to define. Here, choice must be governed, as with everything else, by the taste of the user.