Dr. David Berners (left) is the Universal Audio Director of Algorithm Development; Dr. Jonathan Abel is the co-founder and CTO

Ask the Doctors: Phase Shift and Time Delay
by Dr. Jonathan Abel

This month, the doctors focus on phase shift and time delay. Our readers want to know, "What are they, and what's the difference?"

This question came up in a discussion about guitar effects, and in particular about phasors and flangers, which are very similar beasts. In a flanger, a signal is delayed, scaled and fed back, imposing a comb-like filtering on the input. To make things interesting, the delay is slowly varied over time, causing the spectral features to move. A phasor is almost the same thing, but with a phase shift replacing the time delay.

“A phasor is essentially a flanger, in which the varying time delay is replaced with a varying allpass filter.”

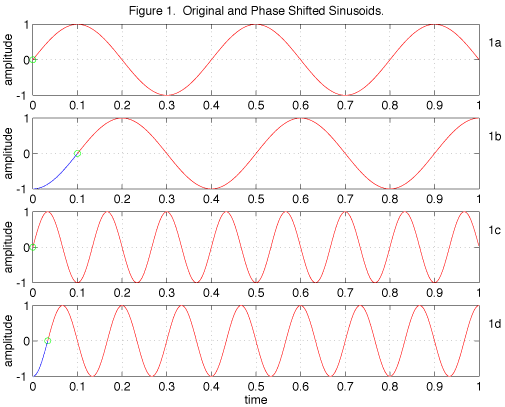
To understand what makes flangers and phasors sound like they do, it is instructive to explore what phase shifting and time-delay operations do to a signal. Consider the sinusoid shown in Fig. 1a, sin(2π·f·t ) and one of its harmics shown in Fig. 1c, sin(2π·2f·t ). The phase of a sinusoid is the starting time of a period of the sinusoid, expressed as a fraction of the period, usually in degrees or radians. Accordingly, a phase shift will slide a sinusoid forward or backward in time some portion of a period φ, sin(2π·f·t - φ ). For example, Fig. 1b shows the sinusoid of Fig. 1a, phase-shifted by 90 degrees, or π/2 radians. In this case, the phase-shifted sinusoid has its positive-going zero crossings a quarter period after those of the original. Similarly, when the harmonic of Figure 1c is phase-shifted 90 degrees, its positive-going zero crossings are delayed a quarter period, as seen in Figure 1d.

Note that a phase shift of 180 degrees or π radians aligns the peaks of the original with the valleys of the phase-shifted signal, giving the negative of the original sinusoid. Stated mathematically: sin(2π·f·t - π) = sin(2π·f·t ) cos(-π) + sin(-π) cos(2π·f·t ) = - sin(2π·f·t ).

Phase shifts applied in succession add, and applying two 180-degree phase shifts leaves a signal unchanged.

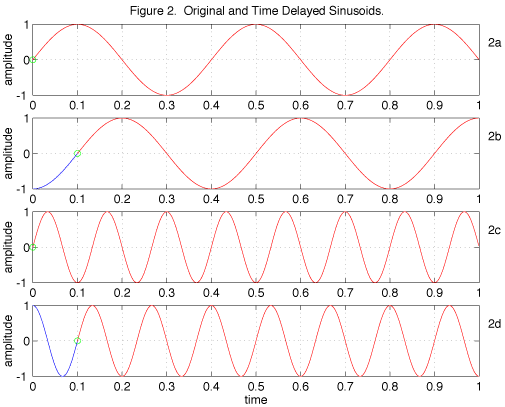
Referring again to Fig. 1, we see that, as the frequency of a sinusoid increases, its period is decreased, and the time delay needed to achieve a given phase shift is decreased. This is in contrast with the action of a pure delay, shown in Figure 2. A pure delay shifts a signal a fixed amount along the time axis, regardless of its frequency.

Figure 2

A little algebra reveals the relationship between time delay and phase shift. Consider a sinusoid sin(2π·f·t ), delayed by an amount φ . Substituting t - τ for t , we have: sin( 2π·f (t - τ ) ) = sin( 2πf t - 2πf τ ) = sin( 2πf t - φ(f ) ).

In other words, a constant time delay of τ results in a frequency-dependent phase shift of 2πf τ . Likewise, a constant phase shift of τ is equivalent to a frequency-dependent time delay of φ / (2πf ).

Consider the sum of a sinusoid and a phase-shifted version: sin( 2πf t ) + sin( 2πf t - φ ).

If the sinusoids are "in phase" (in other words, if the phase shift φ is zero or other integer multiple of 2π), then the two will add to a sinusoid of the same frequency with twice the original amplitude. If, on the other hand, the sinusoids are out of phase (that is, they maintain a relative phase of 180 degrees, or odd integer multiples thereof), then the two will be negatives of each other, and add to zero. For intermediate phase shifts, a sinusoid of amplitude between zero and two results.

What happens if we combine a sinusoid and a delayed version: sin( 2πf t ) + sin( 2πf (t - τ ) ) ?

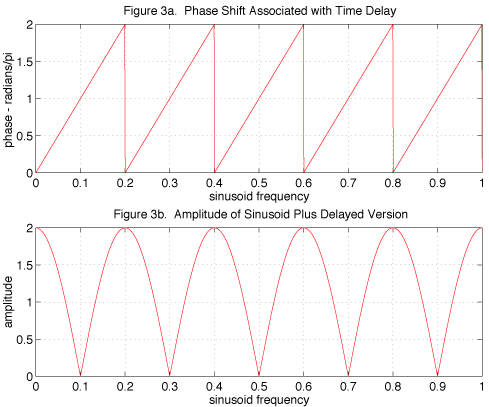
Recall that a time delay τ is like a frequency-dependent phase shift, 2πf τ . Figure 3a shows the phase of the delayed sinusoid as a function of frequency for an example delay. In the plot, any phase that is 2π or greater is made to lie in the interval [0, 2π) by subtracting a multiple of 2π. This can be done since a phase shift of 2π is a shift of one period, and leaves the signal unchanged. In this way, the phase of the delayed sinusoid starts at zero and increases to 2π repeatedly.

Figure 3

So when a sinusoid is added to a delayed version, the result is a sinusoid with an amplitude between zero and two times that of the original. As can be seen in Fig. 3b, at frequencies where the original and delayed sinusoids are in phase, the peaks and valleys of the sinusoids align and their sum is twice the original. At frequencies where the original and delayed sinusoids are out of phase, the peaks of the original fall on the valleys of the delayed version, and cancel.

Figure 4

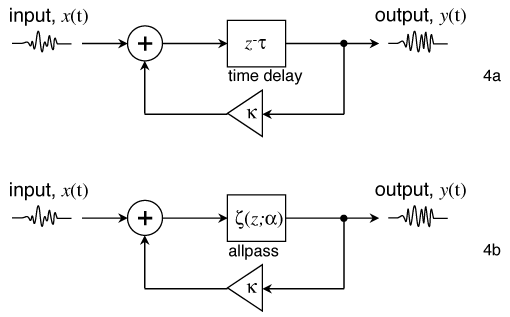
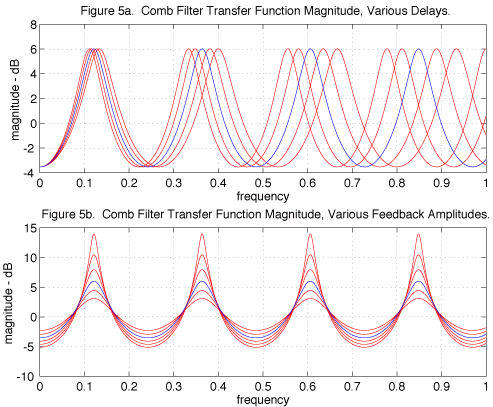
Now consider the filter shown in Figure 4a. An input signal is added to a scaled version of the output; the output is this combination delayed. What would this filter do to an input sinusoid? If the frequency were such that the delayed version was in phase with the input, we would expect the output to be large, as the input is reinforced by its delayed versions. However, at frequencies at which the delayed signal is out of phase with the input, the filter output is expected to be small. This is seen in the filter transfer function, shown in Figure 5a for an example time delay, and a feedback scaling of -0.5. The transfer function, with its regularly spaced peaks and notches gives this filter its name: the comb filter.

The peaks and notches are spaced according to the time delay used. Large time delays result in many narrowly spaced peaks, whereas short time delays give a few widely spaced peaks. By changing the time delay, different frequencies are enhanced and suppressed, as shown in Fig. 5a. By increasing the feedback toward one, the peak heights are increased; by decreasing it toward zero, the transfer function magnitude becomes more smooth, as seen in Fig. 5b.

Figure 5

At the heart of a standard flanger is the comb filter of Fig. 4a, with an LFO sweeping the time delay over a range of values. In this way, the spectral features move up and down in frequency. In a flanger, it is useful to set the time delay range according to the frequency of the first transfer function peak away from DC. For instance, your track might have a lot of energy in the range from 500 to 2,000 Hz. By setting the delay to range from 0.5 to 2.0 ms, the first peak of the transfer function will sweep over that frequency range.

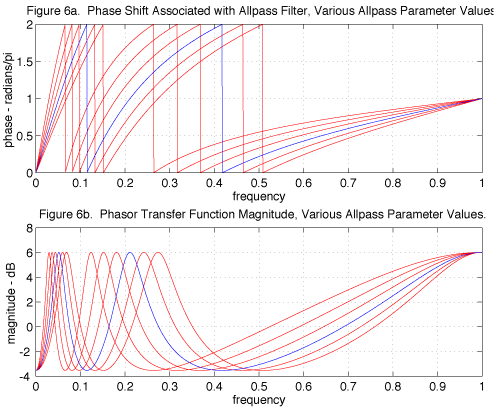
A phasor is essentially a flanger, in which the varying time delay is replaced with a varying allpass filter, as shown in Fig. 4b. The allpass filter imposes a phase that cycles from zero to 2π, much like that of a time delay, and as seen in Fig. 6, a similar series of spectral peaks and valleys results. In the phasor, however, the phase cycles more quickly over some frequency bands compared to others, concentrating its spectral features.